Skip navigation

Research >> Inverse Stefan Problem

Optimal Control of Parabolic Free Boundary Problems


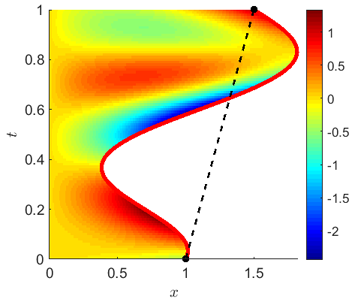
This research is devoted to computational analysis of the inverse Stefan type free boundary problem, where information on the boundary heat flux is missing and must be found along with the temperature and the free boundary. The motivation for this type of inverse problem arose in particular from the modeling of bioengineering problems on the laser ablation of biological tissues through a Stefan problem, where the free boundary s(t) is the ablation depth at the moment t. We pursued the optimal control framework where boundary heat flux and free boundary are components of the control vector, and optimality criteria consist of the minimization of the quadratic declinations from the available measurements of the temperature distribution at the final moment, phase transition temperature on the free boundary, and the final position of the free boundary. The Frechet differentiability and necessary optimality condition in Besov spaces were established under minimal conditions on the data.

We developed a gradient descent algorithm in Hilbert-Besov space based on the formula for the Frechet gradient which is an element of the dual space. By applying Riesz representation theorem, we implement gradient preconditioning to calculate an equivalent form for the Frechet gradient with increased regularity.

Gradient method with and without preconditioning is demonstrated to be an effective method for reconstruction of the local and global optimal control. Calibration of the preconditioning parameter demonstrates that there is an intermediate range of the parameter with best performance with respect to both cost functional and control criteria for the reconstruction of the free boundary. In general, preconditioning with optimal preconditioning parameter improves the convergence rate, but with the expense of increased computational time.

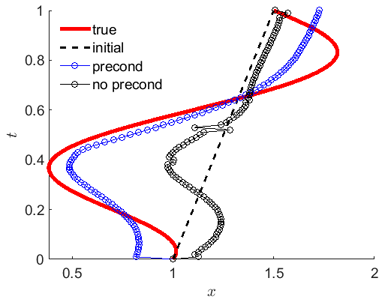
Gradient method for the reconstruction of the free boundary is tested in the presence of additional measurements on the position of the free boundary at some time instances with possible noise. Comparative analysis of alternative approaches when piecewise-linear interpolation of additional measurements is used as either the initial guess or as a regularization centroid of the Tikhonov regularization method. In the former, preconditioning has an advantage if the number of measurements are low, and has no improvement or even a negative effect otherwise. In the latter case, it is demonstrated that the Tikhonov regularization with optimal choice of the regularization parameter has a similar convergence effect as the original method without preconditioning, but with updated initial guess. These outcomes are consistent with sufficiently large Gaussian noise, up to 10%, added to the measurements. Hence, additional measurements of the free boundary have a regularizing effect on the reconstruction of the free boundary.

Gradient method is tested for identification of the free boundary and other control parameters. We developed alternative approaches such as simultaneous identification vs. identification in N-interchanging order or nested optimization, meaning that the identification algorithm switches between control parameters for every N optimization iterations. We pursued two cases with N=1 and N=5 in all model examples. All three methods were accompanied with preconditioning with optimal choice of the parameters. Extensive comparative analysis demonstrates that the advantage of the methods are dependent on model complexity: all three methods worked well in the simplest model, nested optimization has an advantage in the model of moderate complexity, and simultaneous identification has a clear advantage in the most complex model.

Project Collaborators

References